728x90
활성화 함수(Activation Function)의 종류
활성화 함수(Activation Function)란 입력 데이터(input data)의 가중치 합을 출력 신호(Output signal)로 변환하는 함수이다.
대표적인 활성화 함수는 ReLU, 시그모이드(Sigmoid)함수 등이 있다.
1. 시그모이드 함수(Sigmoid Function)
- S자형 곡선 또는 시그모이드 곡선을 갖는 함수이며, 계단함수(Step Function)의 단점을 보안해 준다.
- (계단 함수는 출력값이 0 또는 1의 값만 반환하고, 사이 값은 무시한다.)
-
def logit(a): return 1 / ( 1 + np.exp(-a)) a = np.linspace(-5, 5, 200) plt.plot([-5, 5], [0, 0], 'k--') # x축 plt.plot([-5, 5], [1, 1], 'k-') # (0.1)축 plt.plot([0, 0], [-0.2, 1.2, 'k-') # y축 plt.plot(a, logit(a), "b-", linewidth=2) # Sigmoid plt.grid(True) plt.title("시그모이드 함수 [Sigmoid Function]", fontsize=15) plt.axis([-5, 5, -0.2, 1.2]) plt.show()

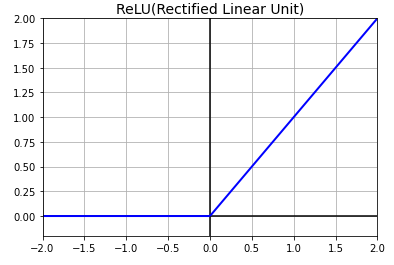
2. ReLU(Rectified Linear Unit)
- 가장 많이 사용하는 활성화 함수이며, 입력값이 0 이상이면 입력값을 그대로 반환하고, 0 이하이면 0을 반환해준다.
-
def relu(a): return np.maximum(0, a) a = np.linspace(-2, 2, 200) plt.plot([-2, 2], [0, 0], 'k-') plt.plot([0, 0], [-0.2, 2.0], 'k-') plt.plot(a, relu(a), "b-", linewidth=2) plt.grid(True) plt.title("ReLU [Rectified Linear Unit]", fontsize=15) plt.axis([-2, 2, -0.2, 2]) plt.show()
3. LeakyReLU (Leaky Rectified Linear Unit)
- ReLU의 단점 중 하나인 Dying 현상(뉴런이 죽는 현상)을 해결하기 위해 0 이하일 때 함수의 기울기가 0이 아닌 약 0.01의 기울기를 주어 죽지 않도록 해준다.
-
def leaky_relu(a, alpha=0.01): return np.maximum(alpha*a, a) plt.plot([-5, 5], [0, 0], 'k-') plt.plot([0, 0], [-0.5, 4.2], 'k-') plt.plot(z, leaky_relu(a, 0.05), "b-", linewidth=2) plt.grid(True) plt.title("Leaky ReLU", fontsize=15) plt.axis([-5, 5, -0.5, 4.2]) plt.show()

4. ELU(Exponential Linear Unit)
- Leaky ReLU와 마찬가지로 Dying ReLU 현상을 막기 위해 나온 개념이다. Leaky ReLU에서는 0 미만에서도 선형적인 구조를 보여주지만 ELU는 비선형 적인 모습을 보여준다.
def elu(a, alpha=1): return np.where(a < 0, alpha * (np.exp(a) - 1), a) plt.plot([-5, 5], [0, 0], 'k-') plt.plot([0, 0], [-2.2, 3.2], 'k-') plt.plot([-5, 5], [-1, -1], 'k--') plt.plot(a, elu(a), "b-", linewidth=2) plt.title("ELU(Exponential Linear Unit)", fontsize=15) plt.axis([-5, 5, -2.2, 3.2]) plt.show()

728x90
'Programming > 머신러닝' 카테고리의 다른 글
| [머신러닝] Warmup Learning Rate (WarmupLR) (0) | 2024.09.06 |
|---|---|
| [머신러닝] 인공 신경망(ANN, Artificial Neural Network) (0) | 2022.02.11 |
| [머신러닝] 강화학습의 분류 (0) | 2022.01.24 |
| [머신러닝] 강화학습 (0) | 2022.01.18 |